[Baekjoon] 이분 그래프
👀 문제 설명
그래프의 정점의 집합을 둘로 분할하여, 각 집합에 속한 정점끼리는 서로 인접하지 않도록 분할할 수 있을 때, 그러한 그래프를 특별히 이분 그래프 (Bipartite Graph) 라 부른다.
그래프가 입력으로 주어졌을 때, 이 그래프가 이분 그래프인지 아닌지 판별하는 프로그램을 작성하시오.
입력
입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V와 간선의 개수 E가 빈 칸을 사이에 두고 순서대로 주어진다. 각 정점에는 1부터 V까지 차례로 번호가 붙어 있다. 이어서 둘째 줄부터 E개의 줄에 걸쳐 간선에 대한 정보가 주어지는데, 각 줄에 인접한 두 정점의 번호 u, v (u ≠ v)가 빈 칸을 사이에 두고 주어진다.
출력
K개의 줄에 걸쳐 입력으로 주어진 그래프가 이분 그래프이면 YES, 아니면 NO를 순서대로 출력한다.
제한
- 2 ≤ K ≤ 5
- 1 ≤ V ≤ 20,000
- 1 ≤ E ≤ 200,000
예제 입력 1
2
3 2
1 3
2 3
4 4
1 2
2 3
3 4
4 2
예제 출력 1
YES
NO
✍🏻풀이
문제 풀이에 앞서, 이분 그래프는 다음과 같은 그래프이다.
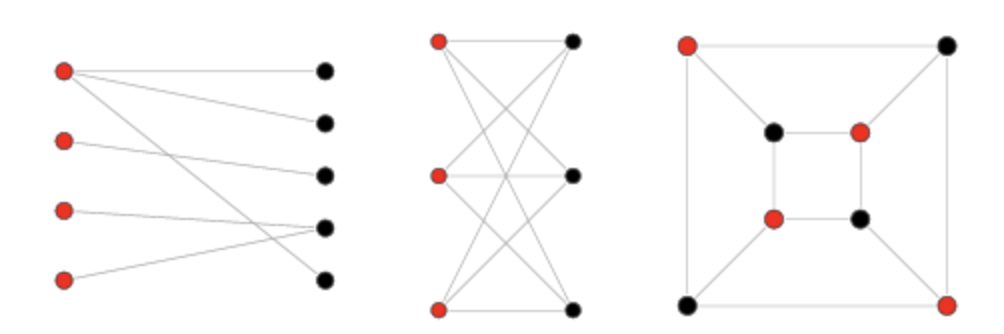
그림과 같이, 인접한 정점끼리 서로 다른 색으로 칠해서 모든 정점을 두 가지 색으로만 칠할 수 있는 그래프를 뜻한다.
-> 참고
이분 그래프인지 확인하는 방법은 그래프 탐색을 이용해 정점을 방문할 때마다 두 가지 색 중 한 가지를 칠하면 된다.
이 때, 현재 정점에서 인접한 정점으로 이동할 때 다른 색을 칠해줘야 한다!
이렇게 다 칠하고 난 후, 자신과 인접한 정점의 색이 같다면 이분 그래프가 아닌 것이다.
* 주의할 점은 연결 그래프와 비연결 그래프 모두 고려해야 한다는 점이다. 비연결 그래프인 경우에는 모든 정점에 대해 확인해야 한다.
위 방법 그대로 문제를 풀면 되는데, 이 문제에서 간선의 개수가 최대 200,000개이므로, 인접 행렬을 사용하면 메모리 초과가 난다.
-> ArrayList 배열로 한 정점과 그에 인접한 정점들을 저장해주면 된다.
ArrayList<Integer>[] graphInfo = new ArrayList[V + 1]; 로 리스트를 생성한 후에, 정보를 저장한다.
예를 들어, 3번 정점이 4, 5번과 연결되어 있다고 가정해보자.
graphInfo[3]은 하나의 ArrayList이고, 이 ArrayList에 4와 5가 차레대로 저장되어 있는 것이다. 즉, graphInfo[3].get(0)은 4, graphInfo[3].get(1)은 5가 될 것이다.
이제 DFS와 graphInfo를 사용해서 정점들을 색칠해주고, 정점들을 다 색칠해준 후에 다시 정점들을 보면서 인접한 정점들이 같은 색인지 확인해주면 된다.
코드
package boj;
// 이분 그래프 (https://www.acmicpc.net/prAroblem/1707 )
import java.util.*;
import java.io.*;
public class BOJ_1707 {
private static int V, E; // 정점의 개수 V와 간선의 개수 E 변수를 선언한다.
private static ArrayList<Integer>[] graphInfo; // 간선 연결 정보 저장 -> 이차원 배열로 하면 메모리 초과 남!!!!
private static int[] color;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); // 입력받기 위해 BufferedReader 객체 생성
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out)); // 출력하기 위해 BUfferedWriter 객체 생성
StringTokenizer st; // 공백을 기준으로 입력받아오기 위해 StringTokenizer 객체 선언
int T = Integer.parseInt(br.readLine()); // 테스트 케이스의 개수를 입력받는다.
for (int tc = 0; tc < T; tc++) { // 각 테스트케이스마다 실행 & 출력
st = new StringTokenizer(br.readLine()); // 공백을 기준으로 입력받아오기 위해 StringTokenizer 객체 생성
V = Integer.parseInt(st.nextToken()); // V 값을 받아온다.
E = Integer.parseInt(st.nextToken()); // E 값을 받아온다.
color = new int[V + 1];
graphInfo = new ArrayList[V + 1];
for (int i = 0; i < E; i++) { // 간선에 대한 정보들을 입력받는다.
st = new StringTokenizer(br.readLine()); // 공백을 기준으로 입력받아오기 위해 StringTokenizer 객체 생성
int u = Integer.parseInt(st.nextToken()); // 시작 정점 정보를 받아온다.
int v = Integer.parseInt(st.nextToken()); // 끝 정점 정보를 받아온다.
// 연결된 정보를 저장해준다.
if (graphInfo[u] == null) {
graphInfo[u] = new ArrayList<>();
}
graphInfo[u].add(v);
if (graphInfo[v] == null) {
graphInfo[v] = new ArrayList<>();
}
graphInfo[v].add(u);
}
for (int i = 1; i <= V; i++) {
if (graphInfo[i] != null && color[i] == 0) { // 1번 정점부터 출발하여, 가능한 정점들을 모두 방문한다.
connected(i, 1);
}
}
// 이분 그래프가 맞는지 확인
boolean poss = isPossible();
bw.write((poss == true ? "YES\n" : "NO\n")); // conn이 true라면, 모든 정점들이 이어져있으므로, 이분 그래프가 아니다. (NO 출력) / false라면, 이분 그래프이므로 YES 출력
}
bw.flush(); // 출력 스트림에 쌓인 애들을 내보내준다.
bw.close(); // BufferedWriter를 다 썼다면 close 해준다.
}
// 이분 그래프가 맞는지 확인 -> 인접한 정점들이 같은 색상이면 이분 그래프가 아니다.
private static boolean isPossible() {
for (int v = 1; v <= V; v++) {
if (graphInfo[v] != null) {
for (int i = 0; i < graphInfo[v].size(); i++) {
if (color[v] == color[graphInfo[v].get(i)]) {
return false;
}
}
}
}
return true;
}
// DFS를 활용해 방문 가능한 정점들을 모두 방문하는 메서드
private static void connected(int cur, int c) { // visited는 정점들이 방문한 것들인지 저장하는 배열, cur은 현재 정점이 몇 번인지 저장하는 변수
color[cur] = c; // 현재 정점 방문 표시 & 색 칠해줌
// 현재 정점과 연결된 정점들 찾기
for (int i = 0; i < graphInfo[cur].size(); i++) {
int next = graphInfo[cur].get(i);
if (color[next] == 0) { // 인접한 정점이 아직 방문하지 않은 곳이라면 해당 정점으로 이동
connected(next, 3 - c); // 현재와 다른 색으로 칠해준다.
}
}
}
}